Atomic Models from Aristotle to Schroedinger
Aristotle
Although the idea of the atom, the smallest, indivisible component of matter, was first proposed in 400 BC, Aristotle didn't like it. He claimed that there was no smallest part of matter and that different substances were made up of proportions of fire, air, earth, and water. As there were of course no experimental means available to test either view, Aristotle's prevailed mainly because people liked his philosophy better.
Dalton
It was not until 1850 that another atomic theory was proposed, this time to explain experimental evidence rather than because it seemed philosophically nice. Dalton stated that all matter is made of indivisible and indestructible atoms, which differ from element to element.The atom, it was assumed, was of uniform density and constitution.
Bohr
That pesky atom, however, refused to cooperate completely. Using the famous gold foil experiment, British experimental physicist Rutherford found evidence that the atom really consisted of a highly dense nucleus and a vast empty space in which the electrons orbited. Bohr seized upon this data and Planck's beginnings at quantum theory and theorized distinct energy levels where electrons could exist. The ground state was where an atom normally was found; the higher energy levels could only be obtained by electrons if they were excited (ie, gained energy, as through a collision). He also discovered that Planck's constant determined the diameter of the atom, and that the atomic spectrum unique to each element was determined by transitions between energy levels (quantum leaps, which are accompanied by the release of a photon.)
de Broglie
Louis Victor Pierre Raymond duc de Broglie added to Bohr's model of the atom by reasoning that, since light could act like a particle, an electron could act like a wave.
Since the energy E of a photon equals Planck's constant times the frequency f, or E=hf, de Broglie reasoned that the momentum p of an electron would equal Planck's constant divided by the wavelength l, or p=h/l. Using this and the reasoning that only a whole number of wavelengths (see picture) would be possible, de Broglie arrived at the same rule for electron orbits as had Bohr.
In other words, a wavelength associated with an electron and derived from its momentum yields a standing-wave pattern identical to Bohr's allowed energy levels. As Einstein put it: "It may look crazy, but it really is sound!"
(In 1929, de Broglie received the Nobel Prize -- the first physicist to do so for his doctoral dissertation.)
Evidence for the de Broglie model came through the Young double slit experiment, an explanation of which can be found at http://www.cmmp.ucl.ac.uk/~ajf/1B23/qm1/node8.html
Schroedinger
But more was still to come: a mathematical model of the atom, provided by Erwin Schroedinger (of cat fame)
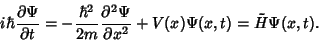
Back to Quantum Mechanics
Back to the Physics Multiverse

Maintained by adamse@technologist.com